Self assembly of supramolecular chains

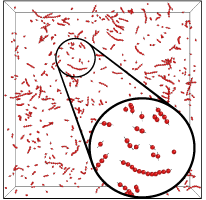We have designed a highly flexible model that can be used to study self-assembly of rigid molecules with specific, directionally dependent, smoothly varying interactions. Supramolecular polymerization is arguably the simplest forms of self-assembly, and although much theoretical and experimental work has been devoted to the subject, it has not received very many computational efforts. For this reason supramolecular polymerization is our first target.

Latent heat and thermal diffusion in nematic liquid crystal nuclei

The growth of nematic liquid crystal nuclei can be described by a power law R(t)=a tⁿ, where the exponent n has been found to smoothly vary between n=1/2 at temperatures close to the phase transition temperature, and n=1 at lower temperatures. The exact physical reason behind the variation in this exponent is not yet known, and although the latent heat generated in the 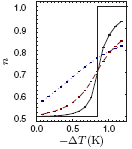transition causes exactly this type of behavior in stronger first order phase transitions, it was commonly thought that this mechanism was too weak in liquid crystals. By using a multiscaled approach to solving the time-dependent Landau-Ginzburg equation for conserved order parameters coupled to a diffusive heat equation, we have shown that latent heat should not be ignored and does lead to power law behavior similar to what is found in experiments.

Burridge Knopoff Model of Multicontact Friction

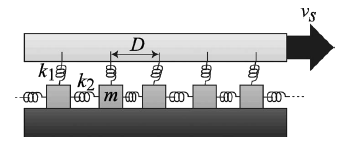
Slowly moving tectonic plates, rough surfaces and flat surfaces with very thin boundary layer lubrication all have in common that the contact interface between the two surfaces moves much like a Caterpillar. Rather than move slowly and steadily, parts of the interface undergo rapid stick-slip motion, while most of the interface stays at rest. The Burridge Knopoff (BK) model was designed to describe this type of stick-slip motion. When the transverse springs are much stronger than the lateral springs the model exhibits avalanche-like behavior: moving blocks cause neighboring blocks to move as well. It is in this incarnation that it is valuable to the earthquake community. If the spring strengths are almost equal, a state more commonly found in frictional systems, the model undergoes a phase transition towards what we have coined "solitary motion": only one of three neighboring blocks is ever in motion in this state. If the frictional system is small enough for temperature effects to be important, the stress in the interface layer decays logarithmically with time after being driven in this solitary state for a while and behaves identical to a theoretical hierarchical glass model.

For a movie of a BK model in the solitary state, click here.